Droplet scRNA-seq is not zero inflated

As scRNA-seq (singel cell RNA sequencing) started to gain popularity users expressed concern about an unexpected number of zero values among gene expressions. That is, for any given gene many cells had not detected the expression, even if it was relatively high in other cells.

It is unclear when this was originally stated, but it has been named the "dropout" problem. A search on Google Scholar will give hundreds of publications discussing the problem of "dropouts" in scRNA-seq, and there are several methods papers explicitly aimed at investigating and dealing with the "dropouts". Typically by imputing zeros to positive values or by stating models which includes a zero-inflation component. These observed zeros ("dropouts") in the data have typically been explained by inefficiencies of molecular reactions, due to the very small volumes of mRNA in individual cells.

In high throughput variants of scRNA-seq assays cells are isolated in (reverse) droplets, within which several molecular reactions occur to eventually give rise to labeled cDNA from expressed genes from each cell. Part of what makes this possible is limiting the sequenced fragments to just single tags from the 3' or 5' end of each transcript. It has recently been observed in statistical analysis that RNA tag counting versions of scRNA-seq data is better explained without additional zero inflation.

Nevertheless, it is common to hear weariness from potential usesrs of droplet based scRNA-seq assays because they are percieved to have a higher amount of "dropouts" than alternative more expensive and manual methods with less throughput.

These observed zeros are consistent with count statistics, and droplet scRNA-seq protocols are not producing higher numbers of "dropouts" than expected because of technical artifacts.

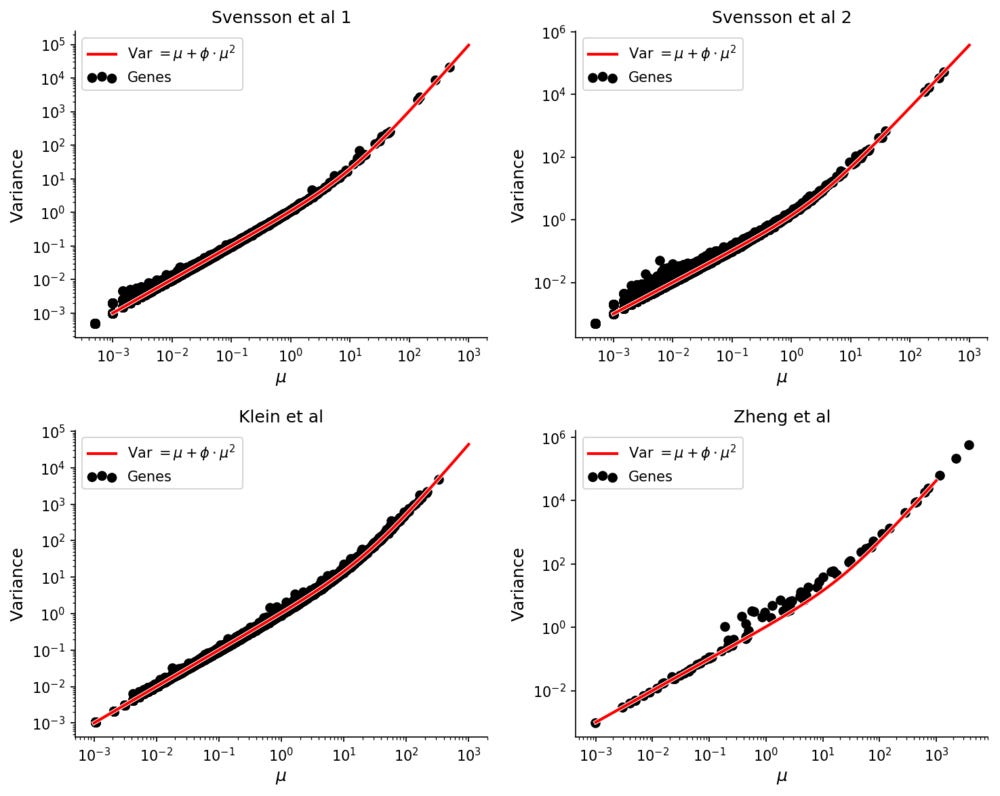
To see this, consider four experiments were solutions of RNA were evenly distributed into droplets, guaranteeing a complete lack of biological variation. One was performed with inDrop (Klein et al), one with 10X Genomics GemCode (Zheng et al), and two with 10X Genomics Chromium (Svensson et al. All datasets have on the order of ~1,000 droplets with RNA, facilitating accurate estimation of e.g. mean or variance for each gene.

It has been observed that expression counts from these technologies follow the negative binomial distribution, in which there is a quadratic mean-variance relationship.

Compared with experiments involving single cells the mean-variance relation is extremely clear in these homogenous datasets.

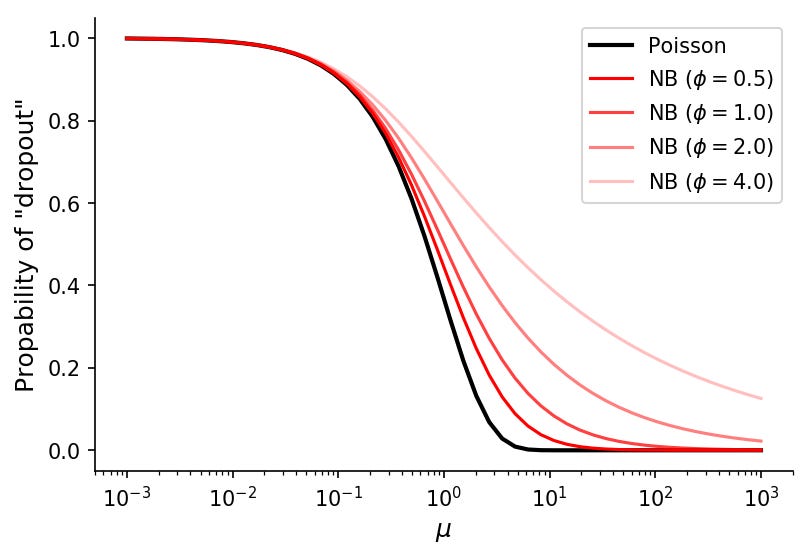
In negative binomial data, the probability of observing a count of \( k \) given the mean \( \mu \) and dispersion \( \phi \) is

\[ P( k \,|\, \mu, \phi) = {k + \phi^{-1} - 1 \choose k} \left( \frac{\mu}{\mu + \phi^{-1}} \right)^k \left( \frac{\phi^{-1}}{\mu + \phi^{-1}} \right)^{\phi^{-1}}. \]

So the probability of \( k = 0 \) is simply

\[ P( k=0 \,|\, \mu, \phi) = \left( \frac{\phi^{-1}}{\mu + \phi^{-1}} \right)^{\phi^{-1}}. \]

With this function we can visualize theoretical "dropout" rates for various means and dispersion values.

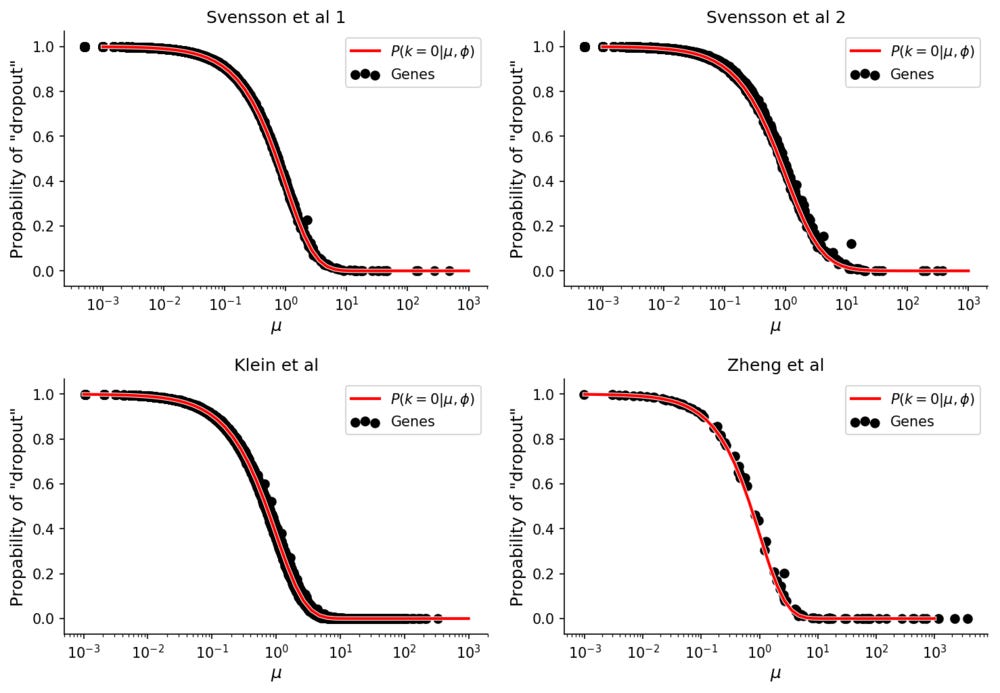
These values can be compared with the empirical "dropout" rate, simply calculated as

\[ \frac{\text{# cells with gene = 0}}{\text{# cells total}} \]

for each gene.

The "dropout" rates for the data without biological variation follows the theoretical prediction. In all datasets the Pearson correlation between theoretical and empirical dropout rates is 99.9%.

Here the \( \phi \) parameter is different for each dataset, and it is possible that this overdispersion is affected by technical factors. There does however not seem to be any technical contribution to zero-inflation, if it is observed it is instead more likely caused by biological heterogeneity.