Solution path for 'Towers of Hanoi'
Solution path for ‘Towers of Hanoi’
A few years ago I figured out a nice strategy for solving the Towers of Hanoi puzzle in the minimum number of moves. By adding a few restrictions to which moves are allowed one gets one single legal move in every (except the initial) step.
To be able to play with the game easily I represented it as integers stacked on eachother, representing the sizes of the corresponding tiles. So for example the initial position for three tiles would look like this:
1 2 3 - - -
For some reason, it occured to me that if one took the sum of every column in such a representation one would get a point in \( \mathbb^3 \), with the property that that \( x + y + z = s \), where \( s \) is the sum of all numbers up to the number of tiles. This means every such point, after every move in the game, will lie in a plane.
If one performs the game for a few low values of \( s \) and plots the path between the points generated by the moves one starts seeing a pattern, which is natural with the symmetric and recursive structure of the game. At the time I imagine a nice fractal pattern would form if one let the number of tiles grow large, but never investigated it.
Now on a whim, after doing some other things in python during the day that in nature reminded me of the Towers puzzle I wrote a script for playing the game for a given number of tiles, saving the point in every step, and plot the path when it was done.
https://gist.github.com/3482cb862dc5e4c3a869
Writing the script was fun, but the results were far from as interesting or pretty as I had thought. Here is a picture of the path for ten tiles.
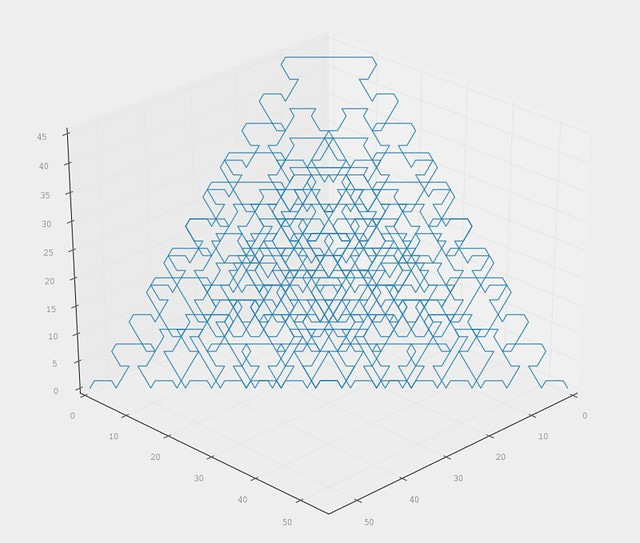
The basic problem, visually, is that the path folds in over it self when the number of tiles get larger than about four.

