The variability of a spoonful of coffee
I like freshly ground coffee, especially made with a French press. The common advice regarding coffee is to dose by weight, due to measurement variability regarding beans in spoons. I was curious how large this variability is.

The different sizes and shapes of the coffee beans makes the volume of the packed beans not correspond to the mass of the coffee, which will be ground to powder.
Different coffee beans are also differently dense, here I’m looking at Brazil Santos coffee.
I made 10 measurements, where I took a level spoon, weighed the contents, then replaced them in my jar of beans before I repeated the measurement.

To quantify the variability, I made a model in Stan. Here a spoonful is modeled normally distributed with a standard deviation parameter which correspond to the between-spoonful variability.
import pystan code = ''' data { int<lower> N; real<lower> y[N]; } parameters { real<lower> mu; real<lower> sigma; } model { // Priors mu ~ uniform(0, 25); sigma ~ uniform(0, 25); // Likelihood y ~ normal(mu, sigma); } ''' data = { 'N': 10, 'y': [13.54, 14.22, 13.63, 13.20, 13.32, 13.23, 13.98, 13.66, 13.51, 14.18] } fit = pystan.stan(model_code=code, data=data) fit Inference for Stan model: anon_model_393a8d8deb17adb090b969fb1275a378. 4 chains, each with iter=2000; warmup=1000; thin=1; post-warmup draws per chain=1000, total post-warmup draws=4000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat mu 13.64 2.3e-3 0.14 13.34 13.55 13.64 13.73 13.91 4000 1.0 sigma 0.43 2.1e-3 0.13 0.26 0.35 0.41 0.49 0.76 4000 1.0 lp__ 5.14 0.02 1.13 2.27 4.74 5.47 5.91 6.22 4000 1.0 Samples were drawn using NUTS(diag_e) at Mon Jul 11 20:54:38 2016. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1).
The y values in the data dictionaries are the weight measurements.
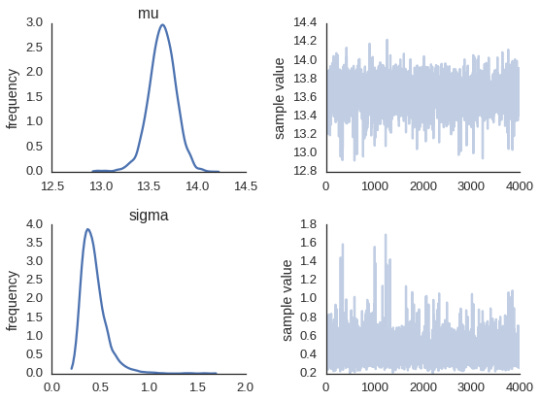
In the end this means that the confidence interval of the spoonful of coffee is between 12.8g and 14.5g.

