Approximate PCA by mini-batch SGD using TensorFlow

In machine learning you usually define a model which has a cost function which you minimize to learn parameters from the data. A very powerful way to do this with large amounts of data is mini-batch stochastic gradient descent (SGD). This means iteratively looking at small random subset of your data, then update parameters using that subset (mini-batch).

I think it's pretty intuitive why this works well; you both need less memory to evaluate the cost function on the mini-batch; and by constantly changing the data we should reach less overfitted results.

This strategy is very well used in supervised classification and regression. Unfortunately in our field of single cell gene expression analysis, these are not the sorts of problems we have. A problem we do have is to learn low-dimensional representations of the data, for example through principal component analysis (PCA).

There are a couple of reasons why mini-batch SGD doesn't make sense for this. Firstly, just making batches over the observations will not help much, because we usually have rather few (hundreds) observations (cells) of many (tens of thousands) variables (genes). Secondly, we need to learn parameters for every observation, so no information would be shared between batches! We would just end up solving many independent problems.

Usually data is represented as a table with observations vs variables. Another way to represent the data is by "long" or "database-style" encoding. (Also known as "tidy" in the R world). Here we store records of values, and indexes for each record indicating which observation and variable the value belongs to. In this formatting it actually makes some sense batching the data!

Recall that in PCA, we want to represent our data Y by

\(Y = W \cdot X,\)

where W contains a weight for each variable, and X has a representative value for each observation. Say that we learn the W and X by batching the long form of the data Y.

From the animation, we notice that the weights for each variable will be learned after each other. So in the beginning of optimization the model will fit the first variable alone. A solution to this is to shuffle the long form of the data.

Now we see there isn't any bias which variables are trained.

I made an implementation of this strategy in TensorFlow. It's not strictly PCA, because the cost function is simply

\(|| y_b - w_b x_b || \cdot \frac{1}{B},\)

where the b subscript indicates that it's from within a batch, and B is the size of the batch. The complete implementation is available here, but the main functional TensorFlow part is the following

N = 2  # Latent space dimensionality

W = tf.Variable(np.random.randn(G, N), name='weights')
x = tf.Variable(np.random.randn(N, S), name='PCs')

sample_idx = tf.placeholder(tf.int32, shape=[None])
variable_idx = tf.placeholder(tf.int32, shape=[None])
y_ = tf.placeholder(tf.float64, shape=[None])

W_ = tf.gather(W, variable_idx)
x_ = tf.gather(tf.matrix_transpose(x), sample_idx)
y_hat = tf.reduce_sum(W_ * x_, 1)

cost = tf.nn.l2_loss(y_ - y_hat) / batch_size

The main point is to use the tf.gather functions to get the sub-tensors for the current batch.

For startars, we apply this to the Iris data:

We see that the cost is going down, and we get a 2-dimensional representation. If we compare to the normal solution to PCA, we see that the our solution finds roughly the same features.

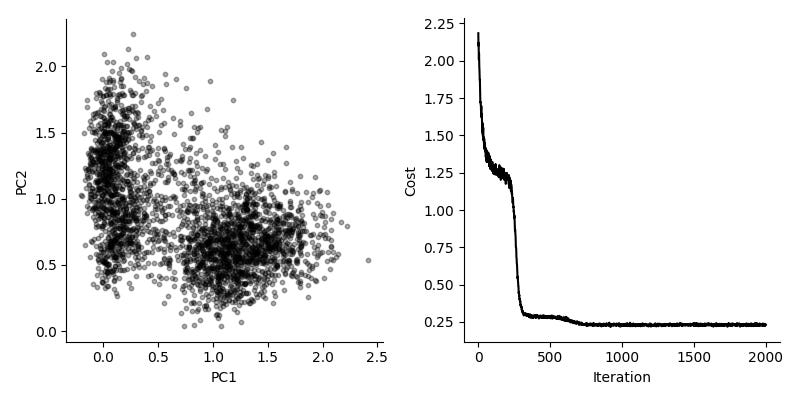
Can we use this for real and interesting data? We evaluate this by considering a dataset by Zeisel et al, consisting of 3,005 single cells from mouse brain. We look at the 3,000 top variable genes, so the long form representation has about nine million rows. Using a batch size of 10,000, we get fairly good results in about 10 seconds.

Again, comparing to the typical solution, here using scikit-learn, we see the same general features.

It should be noted that the scikit-learn PCA is instant for this dataset, it really doesn't make sense to use this mini-batch SGD version in practice. But I think it is interesting because it does show we can use the mini-batch SGD concept for tasks like these. The model we use here could be extended to include known covariates, or it could be used for clustering.